“结绳记事”这一上古时期的信息存储方式，在今天将有望用在通用量子计算机上——物理学家预言，存在一种叫做Fibonacci任意子的粒子，对它们进行编织（braiding）操作可实现抗干扰的量子计算。7月1日，浙江大学物理学院宋超、王浩华研究组与清华大学邓东灵研究组合作在Nature Physics发表论文，在超导量子芯片上实现了Fibonacci任意子的模拟，并成功对其进行了编织操作，“它们在实验观测的拓扑统计行为与理论推算是一致的。”宋超说。作为拓扑量子计算领域重要的基础模型，Fibonacci任意子的成功模拟与编织，意味着向构建通用、容错的量子计算机又迈出了坚实一步。

“结绳记事”的启发

量子计算很强大也很脆弱，它容易受到环境干扰而出错，就像开一辆动力十足但时不时会熄火的汽车。针对这一致命弱点，拓扑量子计算指出了一条解决路径：将信息存放到拓扑的“保护伞”下进行编码和操作，以“屏蔽”任何局域的噪声和扰动。

如何“屏蔽”干扰，上古时期的 “结绳记事”或许蕴藏了独特的答案。诺贝尔物理学奖得主、麻省理工学院弗兰克·维尔切克教授认为：相比于语言、二进制代码和DNA序列等信息存储方式，“绳结”不仅存储信息，还融入了拓扑学——关于形状和稳定的学问，从而获得了不易被改变、抹除或者错误复制等额外优势。“它正在为现代物理学和量子计算提供了一个令人惊讶的模型。”

在科学家眼中，非阿贝尔任意子（Non-Abelian Anyon）具有在量子世界“结绳记事”的潜力，它们是一类在二维平面中“跳舞”的粒子。试想一下，如果在三维世界中交换两个一模一样的小球两次，系统会回到原先的状态；而在二维世界中，交换两个非阿贝尔任意子两次，系统的状态会发生改变，并可被实验探测到，就像对操作产生了“记忆”一样。如果垂直于它们活动的平面画一条时间轴，它们的“舞步”会留下一条连续向上的轨迹，科学家称之为世界线；两个非阿贝尔任意子交换位置时，两条世界线会交叠出一个 “纽结”，见图1。

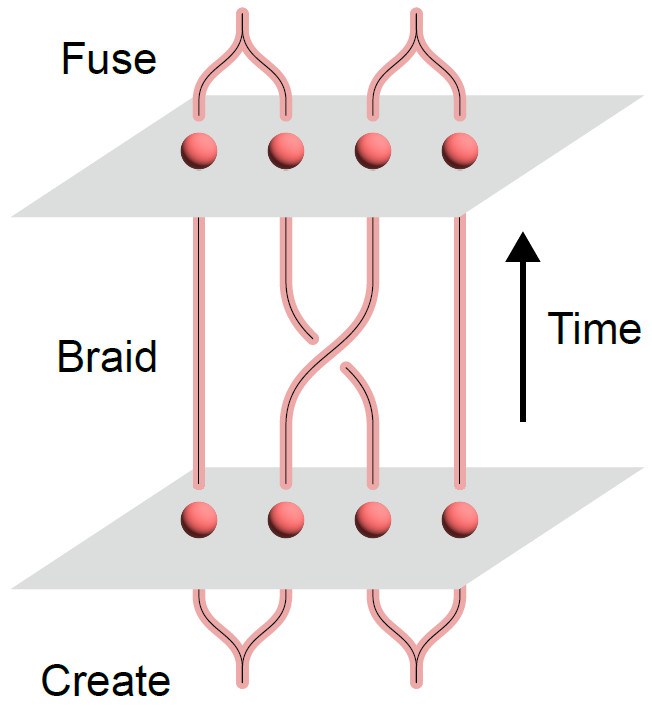
无论是世界线还是“纽结”，它们都为信息存储提供了拓扑保护，使之不容易受到外界的干扰。正因如此，非阿贝尔任意子的长程纠缠序能对环境的局域扰动产生“免疫”，我们可以放心地把信息交给它们。

 “海”上拨“弦”

在本项研究中，合作团队尝试模拟的是Fibonacci任意子，它是非阿贝尔任意子的一种类型，也是拓扑量子计算领域一个重要的基础模型。所谓模拟，是指在超导量子芯片上创造一个量子波函数，来实现目标粒子的特征。我们可以把它想象成一个粒子“角色扮演游戏”，波函数描绘的是角色的发型、服饰、长相等“量子特征”。

论文共同第一作者、博士生徐世波介绍，模拟的依据是著名物理学家文小刚提出的“弦网凝聚”理论。该理论认为：空间本身并不是空的，而是由量子比特组成的“量子比特海”，基本粒子是量子比特海中的气泡和涡旋，而Fibonacci任意子存在于由许多根弦组成的弦网液体（你不妨把它想象成一碗由“弦”组成的意大利螺丝面，“面条”之间能相互连接、分叉、形成网络）中，它们通常出现在一根弦的两端，如图2所示。

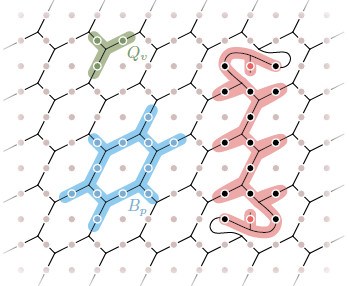
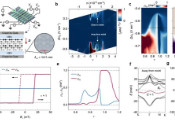
这意味着工作的挑战在于：模拟并不是直接构造出粒子，而是首先要模拟衍生出Fibonacci任意子的“弦”。“弦网液体”的基本单元是一个六边形的蜂窝状结构，而用于模拟的量子比特芯片是四方形的点阵结构。为此，清华大学邓东灵研究组提出实验方案，通过巧妙的倾斜设计，让多个量子比特的活动整体呈现出六边形网格特征，并用一个量子比特来对应“蜂窝”边上的一条“弦”，见图2。通过操控量子比特的状态，可以将“弦”连成特殊的“网”，从而制备出可以容纳Fibonacci任意子的“弦网液体”，图3展示了制备系统基态的量子门线路。

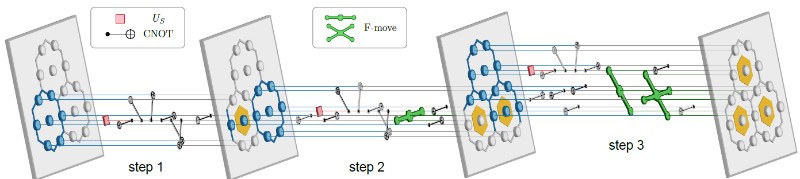
在实验中，研究人员成功模拟了两对Fibonacci任意子。“我们测到了系统基态的拓扑纠缠熵，它代表了存在长程拓扑序，并且与理论演算结果相符，”论文共同第一作者，博士生王可说，“这说明，我们成功通过构建波函数模拟了Fibonacci弦网凝聚液体，在此基础上就能激发Fibonacci任意子。”长程纠缠作为量子拓扑态的基本性质，就像上古时期的“绳结”一样，为信息提供了一个抗干扰的存储空间。

在量子世界“编辫子”

长程纠缠拓扑序为抗干扰的量子计算提供了实现路径，但要打造一台通用的量子计算机，仅仅抗干扰是不够的，我们还要有足够种类的逻辑门来执行操作。“经典计算机之所以是通用型的，是因为所有的计算可以通过逻辑门的组合来完成。”徐世波介绍，如同经典计算机，量子计算机也需要一些特定种类的逻辑门来组合形成所有的量子操作。

“2023年，我们团队完成了非阿贝尔任意子中的伊辛（Ising）任意子的模拟，但它不能构建足够种类的逻辑门。这也是我们在伊辛任意子的基础上又做了Fibonacci任意子的模拟的原因。”

类似于结绳记事，量子计算机中的逻辑门是通过任意子的编织操作实现的。王可介绍，可以在超导量子芯片上打开、关闭甚至挪动量子世界的‘弦’，这些操作可以实现Fibonacci任意子的编织。“我们对这4个Fibonacci任意子进行了两种编织：分别为交换前两个或者中间两个Fibonacci任意子的位置。它们对应了不同的逻辑门操作。” （如图4所示）王可说，在实验中他们还证实了Fibonacci任意子构建通用量子逻辑门的可能性。

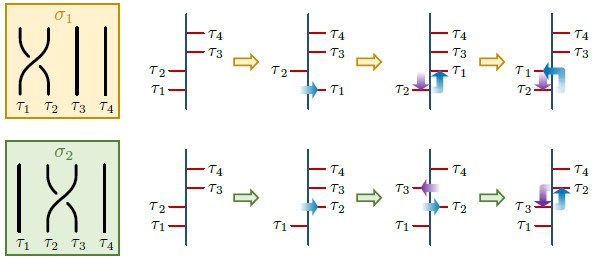
有了不同的逻辑门操作，我们就能像编辫子一样，在量子世界实现不同的操作组合。当“辫子”的数量和长度增长，“辫子”可存储的信息也会指数式增加，即使受到外界扰动，信息也不会丢失或改变——因为受到了拓扑保护。

Fibonacci任意子的成功模拟，向通用容错量子计算迈出了坚实一步，为探索奇异的非阿贝尔拓扑态提供了新方法。宋超也特别说明，这仅仅是对Fibonacci任意子的模拟，它们还未受到拓扑保护。“为实现容错，还需要开发主动纠错等技术，仍然还有许多工作等待我们去完成。”

论文的共同第一作者为浙江大学物理学院博士生徐世波、王可以及清华大学博士后孙正之，实验所用超导量子芯片由浙江大学科创中心李贺康博士制备，通讯作者为浙江大学宋超百人研究员、王浩华教授和清华大学邓东灵教授。

该工作得到了科技部、国家自然科学基金委、浙江省、新基石科学基金会科学探索奖、小米基金会、清华大学笃实专项、上海期智研究院等的支持。