随机数并不新奇，在密码学、信息安全、量子密钥分发、模拟计算、生物仿真等领域有着重要应用。随机数的质量关乎应用安全和结果的可靠性，很多研究者致力找寻到生成真正不可预测的随机数的方案。目前，随机数主要有以下几种典型分类，基于算法的软件随机数、经典物理噪声随机数（电噪声、热噪声等）、量子随机数。

由于研究出发点、应用发展程度不同，当前关于“真随机数”说法指代不一。一种使用语境是，只要能满足现行官方行业随机性检测标准的随机数可称为“真随机数”，其中包括量子随机数、热噪声随机数等。而学术研究认为基于经典物理过程提取的随机数实际仍是可预测的，唯有量子随机数具有内秉真随机性，因为量子天然是“既死又活”的状态，这是量子物理的理论前提和特点。

常见的文献资料多从原理层面阐释量子随机数优越性，实验或应用对比例证显得格外珍贵。硅臻即日起将不定期选编QRNG相关文献，侧重细分应用领域的实验对比，与读者分享交流随机数知识。

本期编译的文献出自内布拉斯加大学奥马哈分校Dario Ghersi等人研究，下为论文主要实验过程和结论的详细介绍。感兴趣的读者可关注硅臻微信公众号，在后台留言“蒙特卡洛论文”，获取下载原文献。

Markov-chain蒙特卡洛模拟准确性在于，随机数生成的试探性变化及其与计算属性的比较。由于过去缺乏以满足计算需求速度生成真正随机数的经济实惠设备，这类模拟通常依赖于伪随机数生成器。随着能够高效生成大量“真”随机数的设备出现，研究者们决定重新审视随机数对蒙特卡洛模拟的影响。

实验对象与方法

随机数发生器选择

量子随机数发生器：研究使用了ID Quantique 公司的量子随机数发生器Quantis（USB版本）。量子随机数发生器源于量子力学的固有随机性和海森堡不确定性原理产生随机比特，Quantis QRNG使用光学系统，通过单个光子在两条路径上的叠加状态来产生随机性。为了消除由于硬件制造过程中的不精确性导致的偏差，Quantis执行了一个去偏步骤。

伪随机数发生器：研究选用了IBM的RANDU、线性同余生成器LCG（Linear Congruential Generator）、带有扰码器的LCGSC64和广为使用的梅森旋转演算法生成器MTG（Mersenne Twister,MTG）。

模拟系统

研究测试了五种随机数发生器在两种体系下的性能表现：水中的刚性钠-二甲基膦酸离子对（DMP-Na）和恒温恒压下的液态甲醇（METH216）。实验使用MMC程序进行模拟。

水中的刚性钠-二甲基膦酸离子对（DMP-Na）：溶质通过Amber84力场来描述，水分子则由SPC模型来表示。为进一步测试QRNG和PRNG，采用了三种不同的增强采样方案：（1）对分子的平动和旋转分别施加力和扭矩偏差；（2）在溶质分子附近更频繁地优先选择水分子；（3）在溶质的紧邻区域减小力偏差，以避免将水分子锁定到离子上。研究人员通过模拟研究了这一离子对在水环境中的若干物理化学性质，如溶质-水相互作用能量、溶质-水+水-水相互作用能量以及溶质质心5.0 Å范围内水分子的平均数量等。

恒温恒压下的液态甲醇（METH216）：针对该系统，分别计算体积、总能量、热容以及甲醇分子的扭转能平均值等物理性质。由于热容与能量波动密切相关，预计它对模拟参数最为敏感。

实验过程与结果

统计测试

NIST测试被密码学界广泛用于评估序列的随机性，实验使用NIST套件对 RNG 进行详尽的统计比较，总计12项测试。其中PRNGs的比特通过将伪随机数的十进制部分转换为二进制得到。NIST测试的零假设是序列具有随机性，备择假设是非随机性。每项测试结果以“通过”（P）或“失败”（F）的形式报告。测试结果汇总于表 1。

DMP-Na体系模拟结果

比较特性：(1) 恒定体积热容；(2) 溶质-水能量；(3) 溶质-水+水-水相互作用能量；(4) 溶质质心5.0 Å范围内水分子的平均数量。

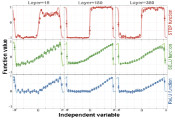
对于每种属性，提取 50 次模拟结束时获取的值，并绘制五种随机数发生器的 DMP-Na体系中四种性质的分布图（图 1）。方框图以粗黑线显示分布的中值，以方框的边界显示第一和第三四分位数（即分布的 25% 和 75%）。

使用 Wilcoxon 检验并应用 Bonferroni 校正进行多重假设检验，对五种随机数发生器得到的分布进行统计比较。表 2 显示了ρ 值，表示基于 PRNG 的分布与基于 QRNG 的分布之间的差异仅由偶然因素造成的概率。

结果表明，RANDU 和 LCG 在 50 次模拟中获得的数值分布明显偏离 QRNG 的结果，而 LSC64SC 和 MTG 与 QRNG 在统计上没有显著差异。更具体地说，当α 值小于 0.05 时，RANDU 与 QUANTUM 在所有四种性质上都有显著的统计学差异，而 LCG 与 QUANTUM 在恒定体积热容和溶质-水+水-水相互作用能量上有统计学差异。

METH216体系模拟结果

在此体系中，实验考虑四种属性：(1) 可压缩性；(2) 扭转能项之和；(3) 甲醇-甲醇相互作用能和扭转能项之和；(4) 平均体积。使用四种 PRNG 和 QRNG 得出的结果见图 3 和图 4，最后一步模拟值的统计比较见表 3。

与DMP-Na体系不同的是，在 METH216 中，只有RANDU与 QRNG 有显著统计差异，而 LCG、LCG64SC 和 MTG 与 QRNG 在统计上没有区别。

测试周期和洗牌的影响

研究探讨了随机数序列周期和洗牌对模拟结果的影响，发现通过在每次重用数据时洗牌能减轻循环使用数据的相关性。与 PRNG 相比，QRNG 的优势是可以轻松控制随机数序列的周期长度。由于每个模拟步骤需要 5-6 个随机数，测试中使用的运行长度会导致多次重复使用同一组随机数。为了发现周期对所研究特性的影响，实验使用少一个数量级（10^7）的量子随机数进行了一组不同的模拟。用 METH216 体系得到的结果与用多十倍的随机数得到的结果在统计上没有区别（所有 ρ值均小于 1，Wilcoxon 检验）。然而，在 DMP-Na 设置中，溶质-水+水-水的相互作用能量在统计学上有所不同（ρ值 < 8.39×10^(-5), Wilcoxon 检验）。

为评估洗牌策略是否可用于减小在DMP-Na设置中观察到的溶质-水+水-水的相互作用能量差异，实验将使用长周期（10^8个量子随机数）得到的结果与使用10^7个随机数（每次使用时对其进行洗牌）得到的结果进行了比较，表明二者并无统计学上的显著差异（ ρ值<0.82，Wilcoxon 检验）。

实验结论

随机数对于生物物理模拟的重要性再怎么强调都不为过。

多项研究证明，劣质 PRNG 会严重扭曲蒙特卡洛模拟的结果。NIST套件对随机数生成器的统计分析与模拟结果比较相吻合。RANDU和LCG在模拟结果中与QRNG有很大偏差，LCGSC64 和广泛使用的 MTG得到的模拟结果与真随机数得到的结果在统计上没有区别，而RANDU和LCG在NIST测试中失败的数量也多于LCGSC64与MTG。

由于PRNG未能通过某些NIST测试的事实，QRNG在密码学应用中可能具有更高的鲁棒性、稳定性。基于本次研究中使用到的劣质PRNG（如LCG）与QRNG之间观察到的较小差异，这些结论可推广至大多数系统。