近日，南方科技大学物理系和量子科学与工程研究院副教授鲁大为团队在量子精密测量领域取得重要进展，在实验中实现了由量子芝诺效应增强的量子精密测量。相关成果以“Entanglement-Enhanced Quantum Metrology in Colored Noise by Quantum Zeno Effect”为题发表在《物理评论快报》（Physical Review Letters)上。

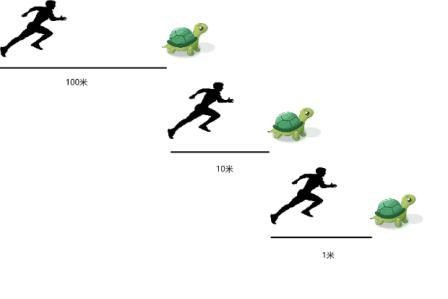
在希腊神话中，阿喀琉斯是一位善跑的英雄。有一次他和乌龟赛跑时，因为他的速度比乌龟快10倍，为了公平起见，乌龟在他前方100米起跑，竞赛要求追者必须先到达被追者的出发点，当阿喀琉斯追到100米时，乌龟已经向前爬了10米，于是，一个新的起点产生了，阿喀琉斯必须继续追，而当他追上乌龟爬的这10米时，乌龟又已经向前爬了1米...... 就这样，乌龟会制造出无穷多个起点，它总能在起点与自己之间制造出一个距离，不管这个距离有多小，只要乌龟不停地向前爬，阿喀琉斯就永远追不上乌龟。这就是古希腊数学家芝诺提出的著名的“芝诺悖论”。当然，在量子世界中，并没有阿喀琉斯和乌龟赛跑。不过当量子系统演化时，频繁的观测会导致系统停留在原来的状态上，这与“芝诺悖论”有异曲同工之妙，也被称为量子芝诺效应(Quantum Zeno Effect)。当然，还有与它相反的版本，频繁观测可以加速量子系统的演化，即量子反芝诺效应(Quantum Anti-Zeno Effect)。

在古埃及时期，人们习惯用绳子来度量土地的长度。而在《史记》大禹治水中也有记载：“左准绳，右规矩，载四时，以开九州。” 这里“准”“绳”便是取平和取直的工具，而“规矩”则是用于测量高低远近的工具。随着科技的进步，人们对测量的要求已经由最初的粗略计量转变为如今的精密测量。在物理学上，测量是一种估计某一特定观测量(或物理参数)的物理过程。测量科学被称为度量学，而测量精度究竟是如何被提升的呢？我们以测量硬币的厚度为例，传统的方式是每次测量一枚硬币的厚度，重复测量N次。假设测量值的期望等于硬币的真实厚度（即无偏估计），那么最终测量厚度的标准差将正比于N^-1/2。为了提高测量的精度，将测量方法改进为每次测量N枚硬币的厚度，重复测量N次后，测量值的标准差将正比于N^-1。这相比于传统方法来说，测量误差降低了N^-1/2。

在真实的物理体系中，以光学上的拉姆齐干涉仪为例，想要测量体系哈密顿量H=ω0σ_z/2中的能量分裂ω0，传统的方法是将初态制备到叠加态上，让其在系统哈密顿量下演化时间t，累积相位ω0t，随后用一个π/2脉冲测量末态的布居 p=[1-cos(ω0t)]/2，重复测量n次后，测量的不确定度将正比于n^-1/2。这就是标准量子极限（Standard Quantum Limit, SQL）。为了提高测量精度，现将初态制备为量子比特最大纠缠态，经过同样演化后测量末态的布居p=[1-cos(ω0t)]/2，得到的测量不确定度正比于n^-1，即海森堡极限（Heisenberg Limit）。这也是量子力学规定的精度上限，通常借助于最大量子纠缠态（例如自旋压缩态、NOON态、GHZ态和Dicke态）等资源去实现。

然而，任何量子系统都不可避免地与周围环境存在相互作用，这种相互作用会导致退相干、振幅衰减、退极化等效应。根据量子系统所处环境是否具有记忆效应，环境噪声可分为马尔可夫和非马尔可夫噪声。马尔可夫噪声不具有记忆效应，也就是环境的状态在前后时刻是没有关联的，是一种理想的简化状态。通常情况下，真实的物理环境带有一定的非马尔可夫性。当然，不管哪种噪声都会使得测量精度无法达到海森堡极限，从而导致量子纠缠态提供的测量优势失效。

2012年，Chin、 Huelga和Plenio从理论上证明了纠缠探针在非马尔可夫噪声中可以超过标准量子极限的精度，达到n^-3/4，这被称为芝诺极限。相比于标准量子极限n^-1/2，芝诺极限带来了n^1/4倍的精度提升，其关键思想是量子芝诺效应可以显著降低退相干误差。这在量子计量界具有重要意义，并引发了一系列后续理论进展，然而，该理论却还没被实验证实过。

要实验证明该理论主要有两大挑战。首先，量子芝诺效应虽然广泛存在于各种量子系统中，但利用它提高量子精密测量的精度需要知道完整的系统与环境相互作用信息。其次，为了证实测量精度能否有n^1/4倍的提升，需要较大的量子比特资源，这也加大了实验的难度。

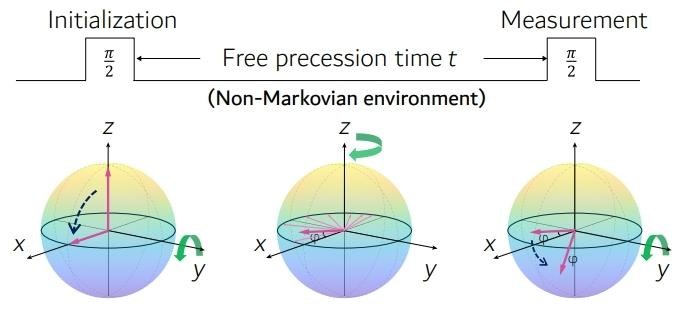
为了解决这两大难题，鲁大为团队采用量子模拟方法来调制噪声模型，并应用bath-engineering技术来模拟高精度的非马尔可夫环境。类似于经典的拉姆齐干涉，研究人员首先将初始态制备到叠加态，然后让其在经过时间调制的哈密顿量H_SB (t)= ω0σ_z /2 +βz (t)σ_z下演化，其中βz (t)是随机误差。虽然单次演化依然是幺正的，但可以通过多次实验取平均值来模拟退相干。Bath-engineering的核心就是在初始的时候制备大量相同的初态，并让它们在不同的哈密顿量H_SB (t)下进行一段时间的演化。由于每个初态感受到的进动频率不一样，它们最终积累的相位也会不同。将末态进行系综（时间）平均，理论上就可以模拟纯退相干环境。

研究人员在核磁共振量子模拟器上进行实验，环境调制是通过使用多达7个核自旋量子比特来实现的。在保证纠缠探针的高保真初始化和读出的情况下，我们观察到，使用纠缠探针时，目标磁场的计量精度正好增强了n^1/4倍，达到了QZE极限。此外，研究人员还设置了一组没有噪声的对照实验，证明纠缠探针能达到海森堡极限，使得计量精度增强了n^1/2倍。这些实验为纠缠增强的量子计量学问题建立了一套完整的实验体系。

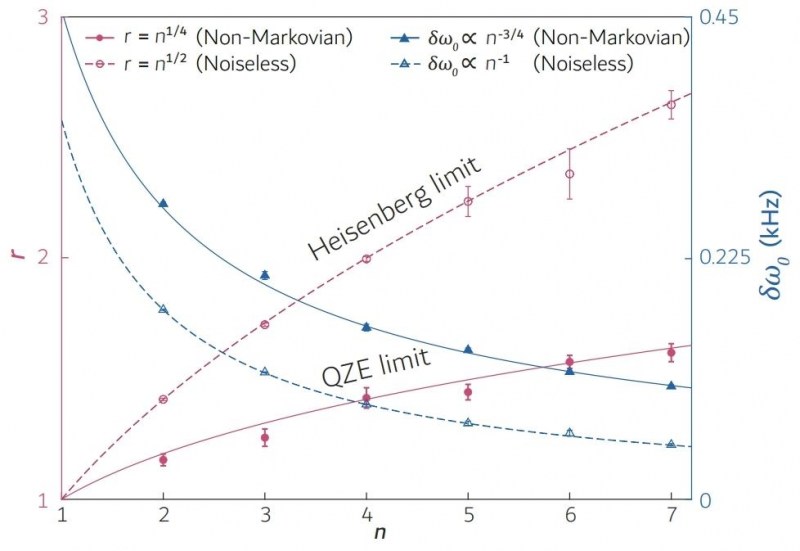
在这项工作中，研究人员应用了一种无需辅助量子比特的bath-engineering技术, 这节省了量子比特资源。同时，实验过程只要求单量子比特绕z轴旋转的操作集合, 这也易于将实验扩展到其他物理体系中。本次实验不仅证明了Chin等人的理论，也为研究人员在其他量子系统中实现非马尔可夫动力学提供了工具，为今后探索噪声环境下的量子精密测量铺平了道路。

该论文的共同第一作者为南科大物理系2019级博士生龙新月、北京师范大学博士生何宛亭和重庆邮电大学讲师张娜娜，理论合作者为北京师范大学副教授艾清，其他合作者包括南方科技大学研究员李俊和副研究员辛涛等。鲁大为和艾清为共同通讯作者，南方科技大学为论文第一完成单位。

以上研究得到了科技部、国家自然科学基金委、广东省科技厅、深圳市科创委、北京市自然科学基金、南方科技大学和北京师范大学等的大力支持。