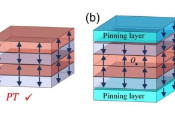
在宏观尺度上看到量子相关性被证明可存在
量子物理学最基本的特征之一是贝尔非局域性,即量子力学的预测无法用任何局域(经典)理论来解释。这在量子信息中具有显着的概念后果和深远的应用。
然而,在我们的日常生活经验中,宏观物体似乎总按照经典物理的规则运行,我们看到的相关性是局域的。真的是这样吗,或者我们可以挑战这种观点吗?在最近发表在《物理评论快报》上的一篇论文中,维也纳大学和奥地利科学院量子光学与量子信息研究所(IQOQI)的科学家们表明,宏观极限上完全保留量子理论的数学结构是可能的。这可能会导致在宏观尺度上观察到量子非局域性。
日常经验告诉我们,宏观系统服从经典物理。因此很自然地期望量子力学必须在宏观极限内重现经典力学。这被称为对应原理,由Bohr在1920年建立。它解释了从量子力学到经典力学的这种转变的一个简单论据是粗粒度机制:如果在宏观系统上进行的测量分辨率有限且无法分辨单个微观粒子,则结果表现经典。
这种应用于(非局域)贝尔相关的论证导致了宏观局域性原理。类似地,时间量子相关性归结为经典相关性(宏观实在论),而量子情境性归结为宏观非情境性。人们坚信量子到经典的转变是普遍的,尽管缺少普遍的证据。为了说明这一点,让我们以量子非局域性为例。
假设我们有两个遥远的观察者,分别是Alice和Bob,他们想要测量他们本地系统之间相关性的强度。我们可以想象一个典型的情况,Alice测量她的微小量子粒子,Bob也做同样的事情,他们结合双方的观察结果来计算相应的相关性。由于他们的结果本质上是随机的(在量子实验中总是如此),他们必须多次重复实验才能找到相关性的平均值。在此上下文中的关键假设是实验的每次运行必须在完全相同的条件下重复并且独立运行,这被称为IID(独立同分布)假设。
例如,在执行随机抛硬币时,我们需要确保每次抛硬币都是公平和无偏见的,从而在多次重复后得到(大约)50%的正面/反面概率。这种假设在宏观极限中还原为经典性的现有证据中起着核心作用。然而,宏观实验考虑了以有限分辨率(粗粒度)打包在一起并一起测量的量子粒子簇。这些粒子彼此相互作用,因此假设微观层面的相关性以独立和相同的对为单位分布是不自然的。如果是这样,如果我们放弃IID假设会发生什么?在大量粒子的限制下,我们是否仍能还原到经典物理学?
Miguel Gallego(维也纳大学)和Borivoje Dakić(维也纳大学和IQOQI)在他们最近的工作中已经表明,如果相关性不是在微观水平上IID分布,那么量子相关性在宏观极限中仍然存在。
Borivoje Dakić说:“在处理大量微观系统时,IID假设并不自然。小量子粒子相互作用非常强烈,量子关联和纠缠随处可见。鉴于这种情况,我们修改了现有的计算,并能够在宏观尺度上找到完整的量子行为。这完全违背了对应原则,而且不会朝经典性质过渡。”
通过考虑涨落可观察量(与期望值的偏差)和某一类纠缠多体态(非IID态),该论文作者表明量子理论的整个数学结构(例如,波恩定律和叠加原理)被保留在极限内。这种被称为宏观量子行为的性质直接使他们能够证明贝尔非局域性在宏观极限下是可见的。
Miguel Gallego说:“在宏观尺度上拥有量子规则真是太神奇了。我们只需要测量波动与预期值的偏差,我们就会在宏观系统中看到量子现象。我相信这将为新的实验和应用打开了大门。”(编译:Qtech)