了解在自然界中发现的或在实验室合成的分子的结构特性一直是材料科学家的工作。但是，随着科学技术的进步，这项工作正变得更加雄心勃勃：去发现具有非常理想特性的新材料。为了系统地完成这一壮举，材料科学家依赖于复杂的模拟技术，这些技术结合了量子力学原理，这些原理与控制分子本身的规则相同。

基于模拟的方法非常成功，以至于整个研究领域被人们称之为材料信息学。但中间也有失败的例子。一个值得注意的例子来自二硅氧烷，它是一种含硅 (Si) 的化合物，由两端各有三个氢原子的Si-O-Si桥组成。该结构足够简单，但众所周知的是，要估计弯曲Si-O-Si桥需要多少能量是出了名的困难。由于计算的特性对参数选择和理论水平的敏感性，会导致实验结果不一致，与理论计算得出的值大不相同。

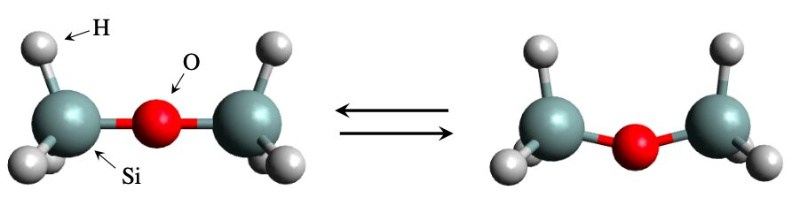
幸运的是，由日本高等科学技术学院副教授Kenta Hongo博士领导的一个国际研究团队现在已经设法解决了这个问题。在他们发表在“PCCP”国际期刊上的研究中，该团队通过使用被称为“第一原理量子蒙特卡罗方法”的最先进的模拟技术实现了这一壮举，并最终克服了其他标准技术无法克服的困难。

但这一切都归结为更好的模拟吗？不完全对。Hongo博士解释道：“得到一个与实验已知值不相符的答案本身并不奇怪。通过更仔细、更昂贵的模拟可以改善一致性。但是对于二硅氧烷，进行更仔细的模拟，一致性实际上会变得更糟。相反，我们的方法取得了很好的效果，对调整参数的依赖性不大，因此我们不必担心调整后的值是否足够。”

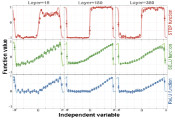
该团队将第一性原理量子蒙特卡罗方法与其他标准技术进行了比较，例如密度泛函理论（DFT）计算，具有单、双替换和非迭代三元组的耦合聚类（CCSD(T)）方法，以及以往研究中的经验测量。这三种方法的差异主要在于它们对基集（Basis-set，一组用于定义量子波函数的函数）的“完备性”的敏感性。

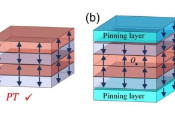
结果表明，对于DFT和CCSD(T)，基集的选择影响了波函数的振幅以及零振幅位置，而使用量子蒙特卡罗方法，它只影响零振幅位置。这使得人们能调整振幅，以使波函数的形状接近精确解。Hongo博士解释道：“振幅的这种自我修复特性可以很好地减少基集依赖性，并降低了计算弯曲能垒时由不完整基组引起的偏差。”

虽然这本身就是一个令人兴奋的进展，但Hongo教授指出了更大的前景。他说：“分子模拟被广泛用于设计新药和催化剂。摆脱了使用它们的根本困难可极大地促进了此类材料的设计。借助我们强大的超级计算机，我们研究中使用的方法可能成为克服此类困难问题的标准策略。”（编译:Qtech）