近日，北京大学物理学院量子材料科学中心进藤龙一（Ryuichi Shindo）课题组2020级博士生肖振宇等人，提出了描述费米子在连续测量下的时间演化的普适随机方程并发现它们的严格解。2025年4月7日，相关成果以“存在测量的量子动力学的普适随机方程”（Universal Stochastic Equations of Monitored Quantum Dynamics）在《物理评论快报》(Physical Review Letters)上在线发表。

测量和幺正时间演化是量子力学中最基本的组成要素。近年来，在存在测量的量子动力学中，人们发现了在平衡态中不存在的物象和非平衡相变普适类。这类新奇的动力学引起了人们的广泛关注 [1]。对它们的研究不仅丰富了科学上对物象以及相变的认识，也为量子态的操控提供了理论指导。费米子作为构成世界的基本粒子，它们在测量下表现出的集体行为，引起了大量研究的兴趣。即使对于没有相互作用的费米子，在测量下也会展现丰富的现象。例如，该类系统是否存在由测量引起的相变存在一定的争议 [2-3]。其对称性的刻画，也没有明确的结果。人们对于这类系统缺乏准确的理解很大程度上是因为缺少对于微观模型的解析结果。

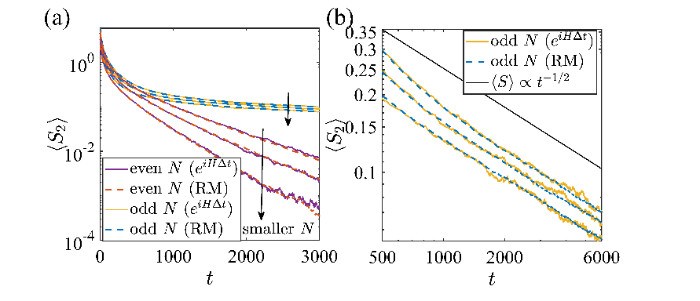
作者们研究了费米子高斯混合态（Gaussian mixed state）在连续测量以及混沌幺正动力学下的时间演化。他们利用随机矩阵理论，推导出了描述它们密度矩阵谱随时间随机演化的普适的福克-普朗克方程（Fokker–Planck equation）。他们还获得了这个方程的严格解。利用这个严格解，他们发现了一些测量下费米子的普适性质。他们发现，动力学演化会在长时间极限下会呈现出奇偶效应。如果系统拥有偶数个费米子自由度，它的熵会在测量下呈现指数衰减。而对于奇数个费米子自由度的情形，系统的熵则以多项式的方式进行衰减，这是一种动力学临界现象的体现 （图1）。此外，他们还发现在短时间极限下，系统的演化会普适地展现出混沌的行为。系统在给定时刻的熵是依赖于测量结果的随机变量，而熵的方差是一个普适的常数，他们解析地得到了这个常数 （图2）。他们将这一现象称之为普适熵涨落，它类似于中观电子传输现象中普适电导涨落。

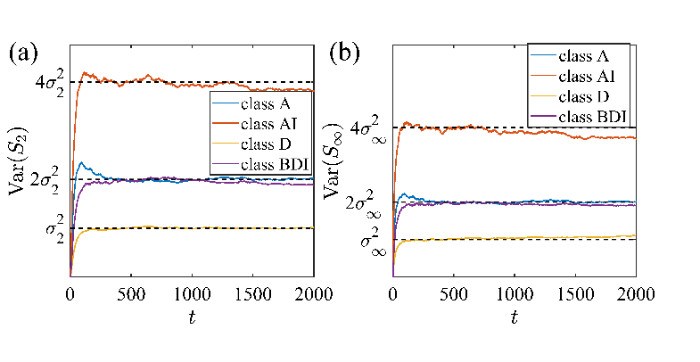
此外，他们系统地研究了如何刻画连续测量下的费米子动力学的对称性。他们发现这类动力学的普适性质只取决于最基本的对称性，如时间反演对称性和粒子空穴对称性。他们研究了有这些基本对称性丰富的动力学，发现他们对应的不同普适类可以反应在他们对应的普适熵涨落上 (图2)。值得注意的是，他们得到的结果是基于一类严格可解模型，但他们对更一般的物理模型进行了大量的数值模型，发现他们解析得到的结果可以普适地描述数值结果。

肖振宇为本论文第一作者兼共同通讯作者。东京大学副教授川畑幸平（Kohei Kawabata）为论文的共同通讯作者。本项工作的合作者还包括上智大学教授大槻東巳（Tomi Ohtsuki）。进藤龙一教授为该工作提供了重要帮助。上述研究工作得到了国家重点研发计划和国家自然科学基金委项目等的支持。