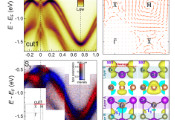
南科大刘奇航课题组在凝聚态体系中的新对称性理论研究取得进展
近日,南方科技大学物理系刘奇航教授课题组在凝聚态体系中的准对称群理论及近似能量简并结构这一方向的研究取得进展,相关成果以“Group Theory on Quasisymmetry and Protected Near Degeneracy”为题发表在学术期刊《物理评论快报》(Physical Review Letters)上。
在物理学中,对称性表示系统或者物理规律在进行特定变换后不发生变化的性质,是现代物理学的一个核心概念。然而,在现实中,大部分对称性都会被破缺,比如人体的左、右半边并非严格满足镜面对称性,而只是近似满足镜面对称性。这些近似存在的对称性会给物理系统带来何种效果,是一个有趣但悬而未决的难题。
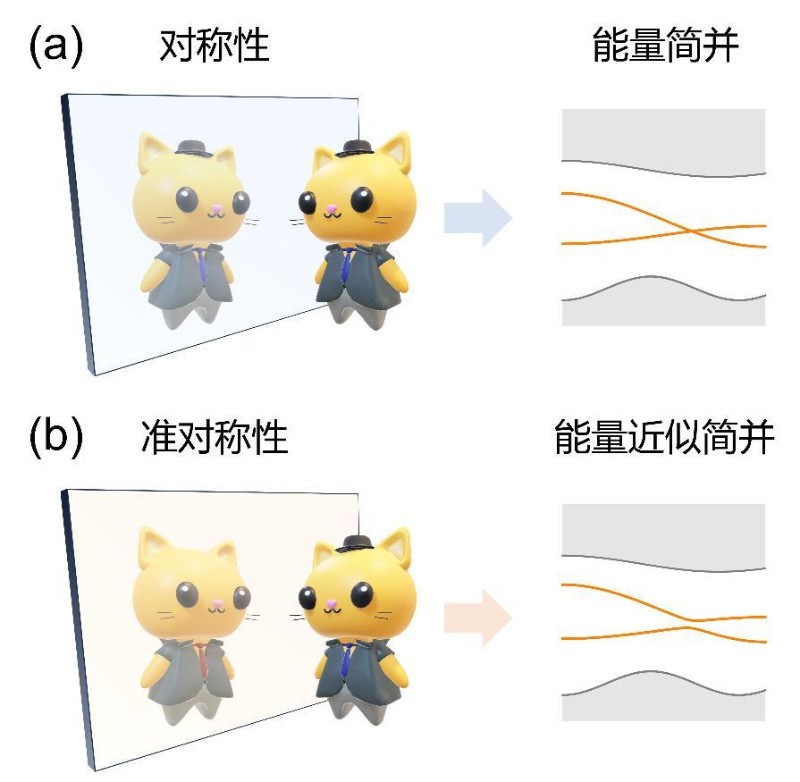
群论是研究对称性的数学工具,基于群论的研究往往为人们带来众多基于对称性的普适结论。群论在描述对称性相关效应存在与否时具有强大的能力。例如,能带简并是否存在,能级跃迁是否允许等。然而,群论通常无法有效区分近似存在的对称性与普遍的对称性破缺。在晶体能带研究中,对称性高的体系允许能量简并(图1a),当体系的对称性因特定因素的加入而破缺时,以往群论能回答该简并能量是否发生劈裂的问题,但是无法回答简并能量劈裂的程度“大或小”,而能量劈裂程度的大小正与近似对称性密切相关。因此,为了能进一步研究凝聚态系统中的近似对称性理论,需要推广现有的群论框架。
在历史发展中,不同研究方向的学者逐渐意识到近似存在的对称性有着不可忽视的影响。如1976年,著名晶体学家Pieter de Wolff为研究调制晶体材料及其X射线衍射谱,引入了赝对称性(pseudo-symmetry)以处理近似存在的晶体平移不变性;1990年,化学家 Paul Mezey 和 Jean Maruani 为研究非刚性分子光学吸收谱中不严格满足的选择定则,引入了使用模糊集合理论描述的模糊对称性(fuzzy symmetry);2022年,Philip Moll、Andrei Bernevig 及刘朝星合作团队基于拓扑半金属材料 CoSi 的量子振荡现象,引入了准对称性(quasisymmetry)以刻画近似简并的拓扑节线。刘奇航研究团队聚焦于凝聚态系统,希望从群论角度得到描述准对称性的普适理论及其与近似能带简并之间的关联,这有助于人们对具有可观贝利曲率及巨大反常输运效应材料的高效判定与设计。
在本研究中,研究团队发展了准对称性的群理论,结合一般性的微扰理论及投影有效哈密顿量的对称性分析,发现了系统哈密顿量的子空间具有哈密顿量不存在的隐藏对称性,而准对称性则是其中可以禁戒一阶微扰项的隐藏对称性,且准对称性在考虑二阶微扰项后被破缺,因此能保护简并能量,打开二阶微扰项量级的极小带隙(图1b)。通过定义新的包含准对称性的群(准对称群)并结合群表示理论,研究团队得到了准对称性存在的必要条件、32个晶体点群中所有允许的准对称性情形,以及准对称群是李群的情形,拓展了以往研究人员对晶体对称性的认知。
基于准对称性的群理论,研究团队预测并解释了狄拉克节线半金属 AgLa 中自旋-轨道耦合驱动的拓扑相变,其中的狄拉克节线在自旋-轨道耦合作用下转变为两个具有6 meV带隙的准狄拉克锥,这种极小的带隙受到空间反演准对称性的保护。这一新理论的提出揭示了固体系统中隐藏的对称性和能级结构之间复杂而精妙的关系,为未来的材料设计和功能性材料研究提供了新的系统方法。
该文章的第一作者为南科大物理系2020级博士研究生李嘉裕(目前在香港大学任职博士后),合作者包括物理系博士后张奥和2019级博士研究生刘云天,刘奇航教授为论文的唯一通讯作者。南科大为论文第一单位。此项工作得到了国家重点研发计划、国家自然科学基金、广东省重点领域研发计划、广东省重点实验室、广东省创新创业团队计划和深圳市科技计划的资助。