意大利INRiM国家计量院的研究团队与牛津大学合作，他们在一项研究中演示了不可逆性与量子力学时间反演对称性定律之间的兼容性。该研究发表在近期的《物理评论快报》上。

关于不可逆性的问题已经有不同的方法可以解决，如统计力学方法、逻辑上不可逆任务的信息理论描述、以及经典和量子热力学第二定律。但无论采用何种方法，不可逆现象的建模与微观尺度上的时间可逆量子定律间总是会产生冲突。

在这项工作中，不可逆性被定义为这样一个事实，即转换(T)可以通过循环机器任意且良好地实现，但它的逆转换(T~)则无法完成。焦耳汤姆逊实验为这种不可逆定义给出了一个典型例子：一定量的水只能被机械地加热(但不能冷却)。

执行转换的循环机器的概念被冯·诺依曼推广到了构造函数(即一个系统能够在另一个系统上执行特定任务，同时保持重复该过程的能力)上。因此，只有当存在能够实现它的构造函数时，才能进行转换。

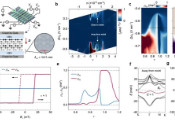
为了演示这种新定义的不可逆性与量子力学的时间反演对称定律能兼容，该团队人员研究了一个以量子均质器为中心的基于量子比特的实验装置(即由一组N个量子比特组成的机器，每个量子比特都能在特定的状态下准备好)。

研究人员通过后续的部分交换(能够部分交换两个量子比特态的量子门)与均质器的N个量子比特相互作用，某些量子比特Q的状态可以绝热地转化为均质器，会在诱导的同时对机器进行轻微的改造。

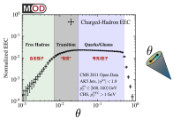
如果T是“纯到混合”转换(Q从纯态转变为最大混合态的变换)，则可以证明该量子均质器被视为一个满足适当构造函数的标准，而对于实现T~(“混合到纯”的情况)则不会出现同样的情况。这意味着，即使T是可能的，它的对应物T~也是不可能。因此，即使在以时间可逆定律来建模的场景中，研究人员也恢复了不可逆性。

为了定量证明这一点，研究人员进行了一项利用高精度的单光子量子比特的实验，该量子比特是由在1550nm处发射光纤耦合单光子的低噪声原型源产生的。

量子比特Q和N=3的量子均质器之间的相互作用是通过级联三个50:50的光纤分束器获得，其输出是由InGaAs/InP单光子雪崩二极管检测。最后，探测器的输出被发送到一个时间标记符合模块上。

通过这样的设置，研究人员首先研究了量子均质器对不同强度的部分SWAP门的性能，随后他们针对T和T~评估了机器在任务实现方面的准确性及其对重复使用的弹性。通过这样做，研究人员证实了他们的理论预测和数值模拟，结果表明虽然T的量子均质器可以作为构造函数，但T~的量子均质器恶化得太快，最终无法执行这样的转换。

这可以看作是基于构造器的不可逆性能与量子理论时间反演对称性相容的明确证明，它为量子力学框架中热力学不可逆性的出现提供了新的视角。（编译:Qtech）