近日，清华大学交叉信息研究院徐勇研究组在拓扑凝聚态物理领域取得重要进展，首次发现对称性保护拓扑相可在无定形里德堡原子链中实现，并发现该系统中存在结构无序诱导的拓扑相变。该成果论文《Symmetry-Protected Topological Phases in a Rydberg Glass（里德堡玻璃中的对称性保护拓扑相）》近日发表在国际学术期刊《物理评论快报》（Physical Review Letters）上。

对称性保护拓扑相是一种新奇的物相，在不破坏对称性的前提下，其基态拓扑性质在连续变化下保持不变，其独特的体边对应关系和拓扑量子相变使其在凝聚态物理研究中备受关注。尽管人们主要在晶体材料中研究拓扑物相，但最近研究表明，拓扑相也可以存在于无相互作用的二维或三维非晶系统中，甚至，这种结构无序可以诱导出拓扑相。但在实验上观测比较困难。随着实验技术的发展，研究人员已经可以将里德堡原子随意摆放，并在一维规则晶格中观测到了拓扑相，这说明里德堡原子为实现结构无序诱导的拓扑相变提供了理想的平台。基于光镊操纵的里德堡原子阵列这一实验体系，该论文在单体和多体层面研究了一维无定形里德堡原子链的拓扑性质,通过使用精确对角化以及矩阵乘积态计算系统基态性质，发现了由手征对称性（单体）和时间反演对称性（多体）保护的无能隙拓扑相（图1左）。与此同时，该论文发现通过增加结构无序的强度使系统由晶态向无定形态转变，系统可经过一个拓扑相变由拓扑平庸态变为拓扑非平庸态，对应的拓扑不变量在相变点处由0跃变至0.5，此现象在单体和多体情况均有发生（图1右）。

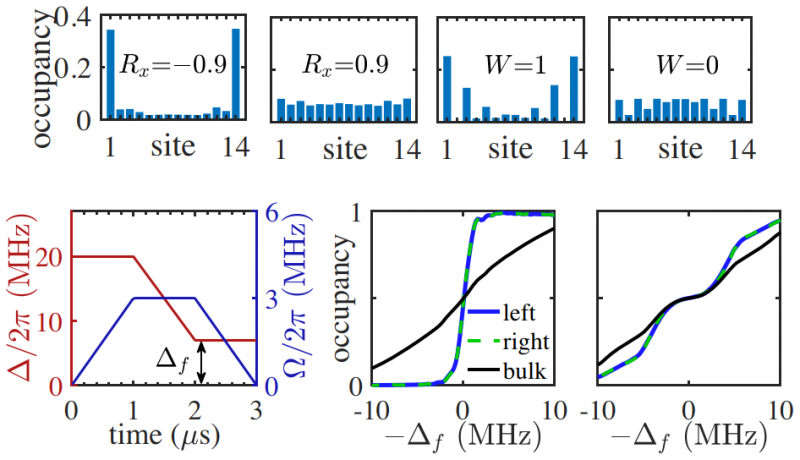
此外，为说明上述理论结果均可被实验探测，该论文模拟了真实实验体系下的动力学演化并计算实验可测量的观测量。模拟结果显示：单体情况下可通过制备零能态并测量其空间分布来刻画系统拓扑，对于拓扑非平庸态，零能态主要集中于边界，而对于拓扑平庸态，其均匀分布于系统中（图2上）；多体情况下的拓扑可以由末态边界占据数随失谐的变化来刻画，系统的非平庸性质体现在失谐为0处边界占据数的突然变化（图2下）。

该论文第一作者为清华大学交叉信息研究院博士生李楷，通讯作者为徐勇助理教授，其他作者包括交叉信息研究院博士生王炅昊和杨炎彬。该项目得到国家自然科学基金、清华大学引进人才启动经费和上海期智研究院的资助与支持。