中国科学技术大学郭光灿院士团队在拓扑量子计算领域取得重要进展。该团队李传锋、许金时、韩永建、孙凯等人与英国利兹大学Jiannis Pachos教授合作，利用自主搭建的光量子模拟器计算了基于马约拉纳零模拓扑结构的琼斯多项式。研究团队通过模拟马约拉纳零模的编织操作，计算了不同拓扑结构的扭结对应的琼斯多项式，所得的琼斯值可以实现对不同扭结结构的区分。该成果12月5日发表在《物理评论快报》上。

琼斯多项式是扭结的一个重要拓扑不变量，它可以被用来区分不同的扭结结构。同时，复杂拓扑结构的琼斯多项式计算是一个#P-hard问题，使用经典算法难以求解。不过，利用马约拉纳零模这一非阿贝尔任意子系统，可以通过构建相应的编织操作来计算扭结的琼斯多项式。不同于三维空间中交换两个全同的玻色子或费米子，系统整体波函数仅会多出一个整体相位；对于二维空间中具有特殊性质的“非阿贝尔任意子”，其交换后的整体波函数会经历一个幺正变换，因此，可以通过对非阿贝尔任意子的交换操作构造量子门，实现具有天然容错特性的拓扑量子计算。已有大量的实验工作研究了马约拉纳零模的物理特性，但由于实验材料及技术的要求极高，通过编织马约拉纳零模实现特定的拓扑量子算法，仍然极具挑战性。

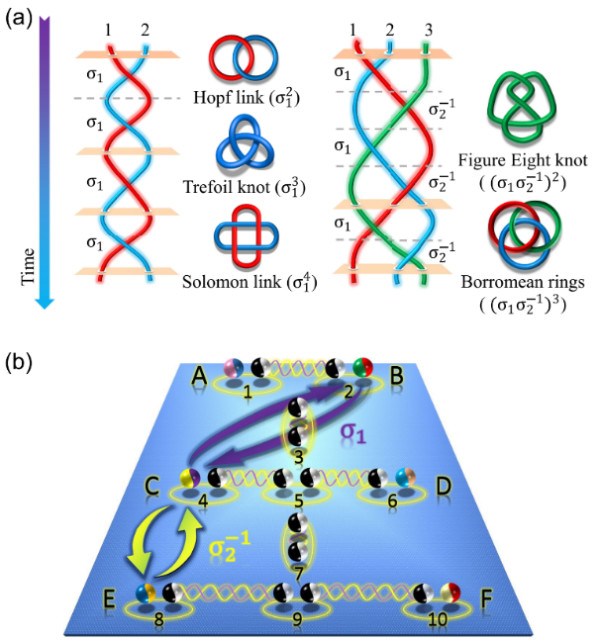
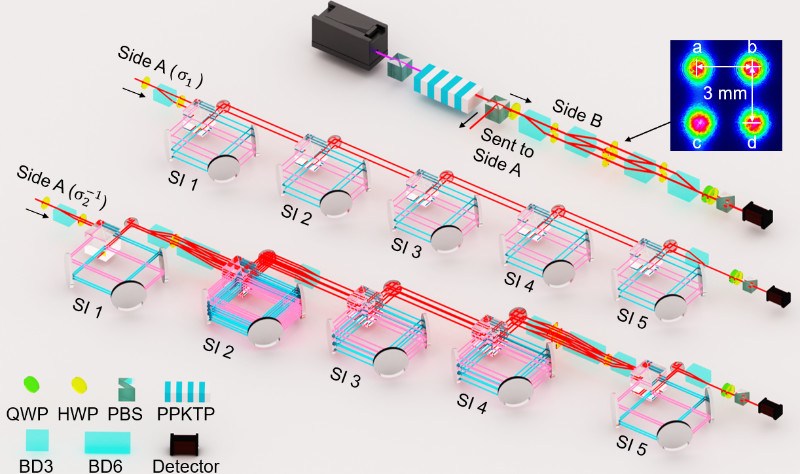
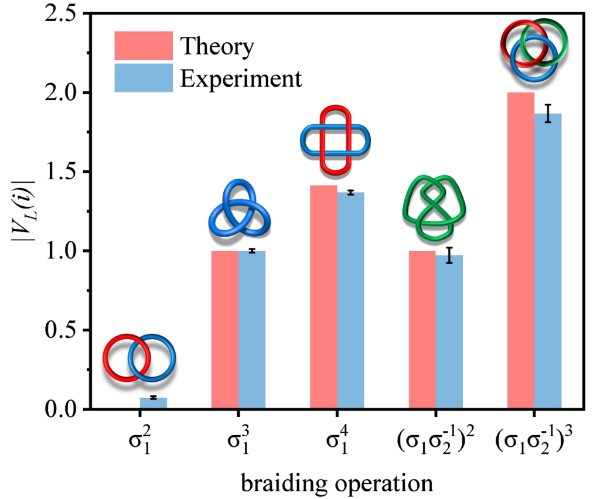
基于光子空间模式的量子模拟器，研究组开展了一系列模拟非阿贝尔任意子拓扑特性的实验研究，先后模拟了单个Kitaev链马约拉纳零模的交换操作[Nat. Commun. 7, 13194 (2016)]、探测了两条Kitaev链模型下马约拉纳零模的非阿贝尔几何相位[Sci. Adv. 4, eaat6533 (2018)]、以及进一步推广到高维情形——仲费米子零模，研究了其编织过程对局域噪声免疫、并且保持了量子互文资源守恒[PRX Quantum 2, 030323 (2021)]。在这些工作的基础上，研究组将之前基于单光子空间模式的编码方式扩展到双光子的空间模式，利用双光子的符合计数进行编码，有效提高了可编码量子态的数量。同时，通过引入基于Sagnac干涉仪的量子冷却装置，将之前工作中的耗散式演化成功转换为非耗散演化，提升了装置对光子资源的回收利用能力，有助于实现多步骤的量子演化操作。这些改进的实验技术极大地提升了自主研制光量子模拟器的能力，为实验模拟三条Kitaev链模型下马约拉纳零模的编织操作奠定了坚实的技术基础。实验中，量子态与编织交换过程的平均保真度均在97%以上。研究组通过组合三条Kitaev链模型下马约拉纳零模不同的编织操作，模拟了五种典型的拓扑扭结，通过将扭结对应的量子末态向初始量子态投影，得到了扭结对应的琼斯多项式的数值解，进一步将不同扭结进行区分。这对于拓扑扭结频繁出现的研究领域，如统计物理、化学分子合成以及DNA复制等均具有重要启示意义。

中国科学院量子信息重点实验室博士研究生李家坤为该论文的第一作者。该工作得到了合肥国家实验室、国家自然科学基金委、安徽省以及中国科学院的资助。