近日，清华大学丘成桐数学科学中心刘子文团队在量子信息和理论物理交叉领域取得重要进展，创新地建立了广义量子纠错性质与系统量子复杂性之间严格联系的普适理论框架，为理解复杂量子系统提供了全新的、统一的视角，这一理论在多体物理和量子引力的研究中具有广泛的应用。

量子纠错编码是量子信息科学与技术的核心研究课题。上世纪末，美国数学家彼得·肖尔（Peter Shor）、加拿大理论物理学家和量子信息科学家丹尼尔·戈特斯曼（Daniel Gottesman）等先驱开拓了这一领域，成为实现量子计算、建造量子计算机的基本方案。近年来，量子纠错思想拓展至前沿物理学研究，为理解奇异物质、黑洞等复杂量子系统注入了全新的活力，极大推动了凝聚态物理、统计物理、高能物理等前沿领域的研究。目前，传统的量子纠错编码研究主要集中于基于稳定子编码数学框架的精确量子纠错的情形。虽然，近似量子纠错的广义情形在实用量子技术和物理方面具有显而易见的重要性，业界仍然对其缺乏系统的理解。

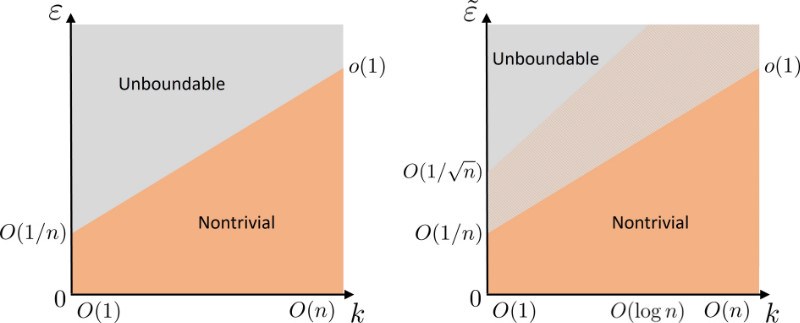
刘子文团队围绕近似量子纠错展开研究，引入了“子系统差异（subsystem variance）”这一新的编码性质，建立了近似量子纠错性质与电路复杂度之间严格的联系，并完成了数学理论的证明，揭示了近似量子纠错编码复杂性“相图”（如图所示），这一理论可广泛应用于数学构造编码、物理系统衍生编码等各类情形。

研究团队证明，如果子系统差异低于O（k/n）阈值（k和n分别为逻辑和物理量子比特数），则编码子空间中的任何量子态都必须高于一定的电路复杂度下限。这一定理可用于标识量子编码和态的非平凡相。根据这一结果，研究团队发现O（k/n）构成了非平凡近似量子纠错码的边界。

这一发现不仅为广义量子纠错编码提供了普适定量的分类标准，还为探索复杂量子系统的量子物理特性开辟了新的途径。研究团队开创性地建立了拓扑序的数种的基本性质之间关联与区别的严格的、定量化的理解，并系统揭示了量子临界系统/共形场论内禀的近似量子纠错编码性质，为通过全息原理理解量子引力提供了新的启示。

该工作拓展了量子纠错编码研究的版图，并揭示了广义量子纠错编码与涵盖凝聚态和高能物理的复杂物理系统之间密切而深刻的联系，深化了对量子信息科技、复杂性科学和物理学之间相互影响的认识，为这些学科的进一步互相推动建立了新桥梁。

9月3日，相关研究成果以“近似量子纠错编码中的复杂性和序”（Complexity and order in approximate quantum error-correcting codes）为题，发表于《自然·物理学》（Nature Physics）。杂志同时发表了该论文的专题介绍文章“连接量子计算、复杂性和物理学的量子编码普适理论”（A general theory of quantum codes connecting quantum computation, complexity and physics）。

清华大学丘成桐数学科学中心助理教授刘子文为论文独立通讯作者。刘子文2023年加入清华大学，主要研究领域为理论量子信息科学，在量子资源、量子编码、量子计算、量子信息与物理及数学的交叉等多个重要方向作出开创性工作。加拿大圆周理论物理研究所博士生易近民为论文第一作者，共同作者包括加拿大英属哥伦比亚大学博士后叶伟成、美国马里兰大学量子信息与计算机科学联合中心主任丹尼尔·戈特斯曼。